Lowest probabilitymass neighbour algorithms: relaxing the metric constraint in distance-based neighbourhood algorithms

Abstract

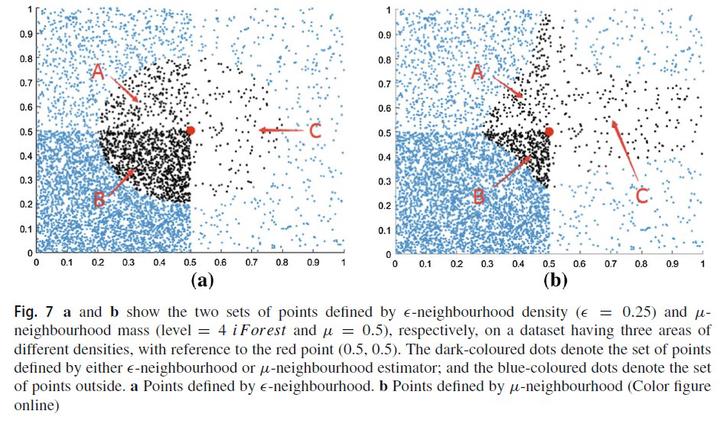
The use of distance metrics such as the Euclidean or Manhattan distance for nearest neighbour algorithms allows for interpretation as a geometric model, and it has been widely assumed that the metric axioms are a necessary condition for many data mining tasks. We show that this assumption can in fact be an impediment to producing effective models. We propose to use mass-based dissimilarity, which employs estimates of the probability mass to measure dissimilarity, to replace the distance metric. This substitution effectively converts nearest neighbour (NN) algorithms into lowest probability mass neighbour (LMN) algorithms. Both types of algorithms employ exactly the same algorithmic procedures, except for the substitution of the dissimilarity measure. We show that LMN algorithms overcome key shortcomings of NN algorithms in classification and clustering tasks. Unlike existing generalised data independent metrics (e.g., quasi-metric, meta-metric, semi-metric, peri-metric) and data dependent metrics, the proposed mass-based dissimilarity is unique because its self-dissimilarity is data dependent and non-constant.