Adversarial decision strategies in multiple network phased oscillators: the Blue-Green-Red Kuramoto-Sakaguchi model
Abstract
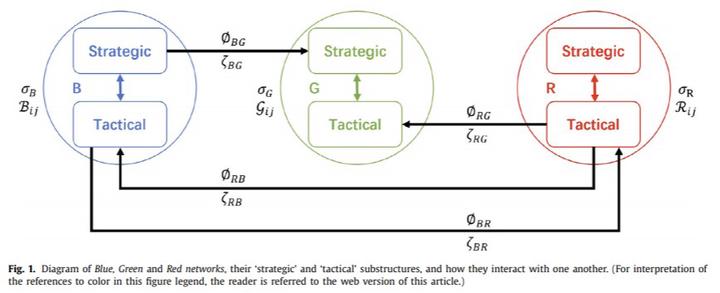
We consider a model of three interacting sets of decision-making agents, labeled Blue, Green and Red, represented as coupled phased oscillators subject to frustrated synchronisation dynamics. The agents are coupled on three networks of differing topologies, with interactions modulated by different cross-population frustrations, internal and cross-network couplings. The intent of the dynamic model is to examine the degree to which two of the groups of decision-makers, Blue and Red, are able to realise a strategy of being ahead of each others’ decision-making cycle while internally seeking synchronisation of this process – all in the context of further interactions with the third population, Green. To enable this analysis, we perform a significant dimensional reduction approximation and stability analysis. We compare this to a numerical solution for a range of internal and cross-network coupling parameters to investigate various synchronisation regimes and critical thresholds. The comparison reveals good agreement for appropriate parameter ranges. Performing parameter sweeps, we reveal that Blue’s pursuit of a strategy of staying too-far ahead of Red’s decision cycles triggers a second-order effect of the Green population being ahead of Blue’s cycles. This behaviour has implications for the dynamics of multiple interacting social groups with both cooperative and competitive processes.